- Published on
Data Analysis Wahl-O-mat: Part 1
- Authors

- Name
- Avasdream
- @avasdream_
If you think at the moment: "This is way too much text for my attention span" -> here you go
What is the Wahl-O-mat?
Wahl-O-Mat is an interactive online tool developed by the German Federal Agency for Civic Education (Bundeszentrale für politische Bildung). It is designed to help voters understand the political positions of various parties in upcoming elections, such as the European elections in 2024. Users respond to a series of statements, and Wahl-O-Mat compares their answers to the platforms of different political parties, providing a visual representation of which parties align most closely with their views. This tool aims to facilitate informed voting decisions. For more details, visit Wahl-O-Mat.
--ChatGPT, 25.05.2024
Data is beautiful
While playing with the Wahl-O-Mat for the upcoming European elections, I discovered that all calculations for the results are done client-side, which makes sense for privacy reasons. This ensures that sensitive and election related data isn't stored on a state-owned server. I was pleased to find that extracting the data from the JavaScript files was straightforward. However, before diving into this tedious task, I searched online and found that a GitHub user named "gockelhahn" had already formatted the data and made it public, covering elections back to 2022. Thanks a lot and check it out here.

First look at the data:
The Wahl-O-Mat utilizes several JSON files to match users' opinions with political parties. Here's a breakdown of the key files and their contents:
party.json: Lists all political parties with unique IDs, short names, and full names. This helps in referencing parties across different files.
[
{
"id": 0,
"name": "CDU / CSU",
"longname": "Christlich Demokratische Union Deutschlands / Christlich-Soziale Union in Bayern e.V."
},
{ "id": 1, "name": "GRÜNE", "longname": "BÜNDNIS 90/DIE GRÜNEN" },
{ "id": 2, "name": "SPD", "longname": "Sozialdemokratische Partei Deutschlands" }
]
statement.json: Contains the statements on various issues that users will respond to. Each statement has an ID, category, label, and text.
[
{
"id": 0,
"category": null,
"label": "EU-Steuern",
"text": "Die EU soll eigene Steuern erheben dürfen."
},
{
"id": 1,
"category": null,
"label": "Verbrennungsmotoren",
"text": "Fahrzeuge mit Verbrennungsmotoren sollen auch nach 2035 in der EU neu zugelassen werden können."
},
{
"id": 2,
"category": null,
"label": "Seenotrettung",
"text": "Die EU soll eine eigene Seenotrettung im Mittelmeer aufbauen."
}
]
comment.json: Stores the arguments for each party's position on the statements. The ID corresponds to the statement ID.
[
{
"id": 0,
"text": "\"Wir wollen das bestehende Finanzierungssystem der EU beibehalten. Die EU soll sich aus den Beiträgen der Mitgliedstaaten, den Mehrwertsteueranteilen der Mitgliedstaaten sowie Zöllen finanzieren.\""
},
{
"id": 1,
"text": "\"Wir stehen zum Auto, unabhängig von der Antriebsart. Wir wollen das Verbrennerverbot wieder abschaffen. Unser Ziel ist es, die deutsche Spitzentechnologie des Verbrennungsmotors zu erhalten und technologieoffen weiterzuentwickeln. Synthetische Kraftstoffe spielen dafür eine zentrale Rolle. Wir schreiben keine Technologien vor.\""
},
{
"id": 2,
"text": "\"Die Wiederaufnahme der staatlichen Seenotrettung würde das falsche Signal setzen. Je mehr Schiffe im Mittelmeer zur Rettung unterwegs sind desto mehr Menschen machen sich mit seeuntauglichen Booten auf den gefährlichen Weg und bringen sich in Lebensgefahr.\""
}
]
opinion.json: Contains each party's stance on the statements. The IDs link to party and statement IDs, with answers coded as 1 for yes, 0 for no, and 2 for neutral.
[
{ "id": 0, "party": 0, "statement": 0, "answer": 1, "comment": 0 },
{ "id": 38, "party": 1, "statement": 0, "answer": 0, "comment": 38 },
{ "id": 76, "party": 2, "statement": 0, "answer": 1, "comment": 76 },
{ "id": 114, "party": 3, "statement": 0, "answer": 1, "comment": 114 },
{ "id": 152, "party": 4, "statement": 0, "answer": 0, "comment": 152 },
{ "id": 1140, "party": 30, "statement": 0, "answer": 2, "comment": 1140 },
{ "id": 608, "party": 16, "statement": 0, "answer": 2, "comment": 608 }
]
answer.json: Defines the possible answers users can select, which are matched against the parties' positions.
[
{ "id": 0, "message": "Stimme zu" },
{ "id": 1, "message": "Stimme nicht zu" },
{ "id": 2, "message": "Neutral" }
]
First experiment
Let's first have a look at the similarity of political parties in their overall opinions. This will be done by first merging the JSON data into dataframes we can work with, then translating the answers from the values 0, 1, 2 to -1, 0, 1, and finally calculating the Pearson correlation between the parties. To visualize this, we will use a heatmap.
# File paths
data_folder = "data"
files = {
"overview": f"{data_folder}/overview.json",
"party": f"{data_folder}/party.json",
"statement": f"{data_folder}/statement.json",
"answer": f"{data_folder}/answer.json",
"opinion": f"{data_folder}/opinion.json",
"comment": f"{data_folder}/comment.json"
}
# Load JSON data
def load_json(file_path):
with open(file_path, 'r') as file:
return json.load(file)
overview = load_json(files["overview"])
parties = load_json(files["party"])
statements = load_json(files["statement"])
answers = load_json(files["answer"])
opinions = load_json(files["opinion"])
comments = load_json(files["comment"])
We are loading the data from the JSON files into Python dictionaries. Next, we will convert this data into pandas DataFrames for easier analysis.
# Convert to DataFrame for analysis
parties_df = pd.DataFrame(parties)
statements_df = pd.DataFrame(statements)
answers_df = pd.DataFrame(answers)
opinions_df = pd.DataFrame(opinions)
comments_df = pd.DataFrame(comments)
# Merge data for analysis
merged_df = opinions_df.merge(parties_df, left_on='party', right_on='id', suffixes=('_opinion', '_party'))
merged_df = merged_df.merge(statements_df, left_on='statement', right_on='id', suffixes=('', '_statement'))
To make it easier to work with we create a pivot table where each row represents a statement and each column a party. The values in the table represent the party's stance on the statement.
party_positions = merged_df.pivot_table(index='statement', columns='name', values='answer', aggfunc='first')
Here is the table with the party positions:
[1292 rows x 12 columns]
name ABG AfD BIG BSW BÜNDNIS DEUTSCHLAND Bündnis C CDU / CSU DAVA DIE LINKE DKP ... PdF PdH SGP SPD TIERSCHUTZ hier! Tierschutzpartei V-Partei³ Volt dieBasis ÖDP
statement ...
0 1 1 1 1 1 1 1 1 0 1 ... 1 0 1 1 1 0 1 0 1 0
1 0 0 1 0 0 0 0 0 1 1 ... 0 0 0 1 0 1 1 1 0 1
2 1 1 0 1 1 1 1 0 0 0 ... 0 0 0 0 0 0 0 0 1 0
3 1 1 1 1 1 0 0 1 1 1 ... 0 2 1 0 1 0 2 0 1 2
4 0 1 0 1 1 1 1 0 0 0 ... 0 1 0 1 0 0 0 0 0 0
5 0 0 1 1 1 0 1 1 1 2 ... 1 1 1 1 1 1 1 1 0 1
6 1 1 1 1 1 1 1 1 0 0 ... 0 0 0 0 1 0 0 0 1 0
7 1 0 0 0 0 0 0 0 1 1 ... 2 2 1 2 1 1 1 1 0 1
8 1 1 0 1 1 1 1 1 0 0 ... 1 1 1 1 1 0 0 0 1 0
9 1 1 0 1 1 1 0 0 1 1 ... 0 0 1 0 1 0 0 0 1 0
10 1 0 2 1 0 1 0 1 1 1 ... 1 1 1 1 2 1 1 1 1 1
11 1 1 0 2 0 1 0 0 1 1 ... 0 0 1 0 1 2 0 0 1 0
Now we are replacing the original values with new ones to standardize the data for further analysis. Using inplace=True means the changes are made directly in the original table rather than creating a new one.
- 0 becomes 1
- 1 becomes -1
- 2 becomes 0
party_positions.replace({0: 1, 1: -1, 2: 0}, inplace=True)
So the table looks like that and as you can see the values in the original table have been replaced:
[38 rows x 34 columns]
name ABG AfD BIG BSW BÜNDNIS DEUTSCHLAND Bündnis C CDU / CSU DAVA DIE LINKE DKP ... PdF PdH SGP SPD TIERSCHUTZ hier! Tierschutzpartei V-Partei³ Volt dieBasis ÖDP
statement ...
0 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 ... -1 1 -1 -1 -1 1 -1 1 -1 1
1 1 1 -1 1 1 1 1 1 -1 -1 ... 1 1 1 -1 1 -1 -1 -1 1 -1
2 -1 -1 1 -1 -1 -1 -1 1 1 1 ... 1 1 1 1 1 1 1 1 -1 1
3 -1 -1 -1 -1 -1 1 1 -1 -1 -1 ... 1 0 -1 1 -1 1 0 1 -1 0
4 1 -1 1 -1 -1 -1 -1 1 1 1 ... 1 -1 1 -1 1 1 1 1 1 1
5 1 1 -1 -1 -1 1 -1 -1 -1 0 ... -1 -1 -1 -1 -1 -1 -1 -1 1 -1
6 -1 -1 -1 -1 -1 -1 -1 -1 1 1 ... 1 1 1 1 -1 1 1 1 -1 1
7 -1 1 1 1 1 1 1 1 -1 -1 ... 0 0 -1 0 -1 -1 -1 -1 1 -1
8 -1 -1 1 -1 -1 -1 -1 -1 1 1 ... -1 -1 -1 -1 -1 1 1 1 -1 1
9 -1 -1 1 -1 -1 -1 1 1 -1 -1 ... 1 1 -1 1 -1 1 1 1 -1 1
10 -1 1 0 -1 1 -1 1 -1 -1 -1 ... -1 -1 -1 -1 0 -1 -1 -1 -1 -1
In the next line the Pearson correlation is calculated. The correlation matrix shows how similar each pair of parties is. A value of 1 means the two parties always agree, -1 means they always disagree, and 0 means there's no relationship.
correlation_matrix = party_positions.corr(method='pearson')
The one line of code above does quite some heavy lifiting for us. So here is the code without abstraction:
def manual_pearson_correlation(x, y):
mean_x = np.mean(x)
mean_y = np.mean(y)
numerator = np.sum((x - mean_x) * (y - mean_y))
denominator = np.sqrt(np.sum((x - mean_x) ** 2) * np.sum((y - mean_y) ** 2))
return numerator / denominator if denominator != 0 else 0
# Calculate the correlation matrix manually
party_names = party_positions.columns
num_parties = len(party_names)
correlation_matrix_manual = np.zeros((num_parties, num_parties))
for i in range(num_parties):
for j in range(num_parties):
correlation_matrix_manual[i, j] = manual_pearson_correlation(party_positions.iloc[:, i], party_positions.iloc[:, j])
This code defines a function to manually calculate the Pearson correlation coefficient between two sets of data, x and y, by finding their means, computing the sum of their centered products, and normalizing by their standard deviations. It then uses this function to compute the correlation matrix for a DataFrame party_positions, where each entry represents the linear correlation between different columns (or parties) in the DataFrame. The resulting correlation matrix correlation_matrix_manual shows the pairwise correlations for all columns, with each element computed using the custom Pearson correlation function.
To visualize the data we use a heatmap where alignment is color coded in blue and red.
plt.figure(figsize=(14, 10))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', cbar=True, linewidths=.5)
plt.xlabel('Parties')
plt.ylabel('Parties')
plt.title('Correlation Matrix of Party Positions')
plt.xticks(rotation=90)
plt.yticks(rotation=0)
plt.show()
And here is the correlation matrix visualized:
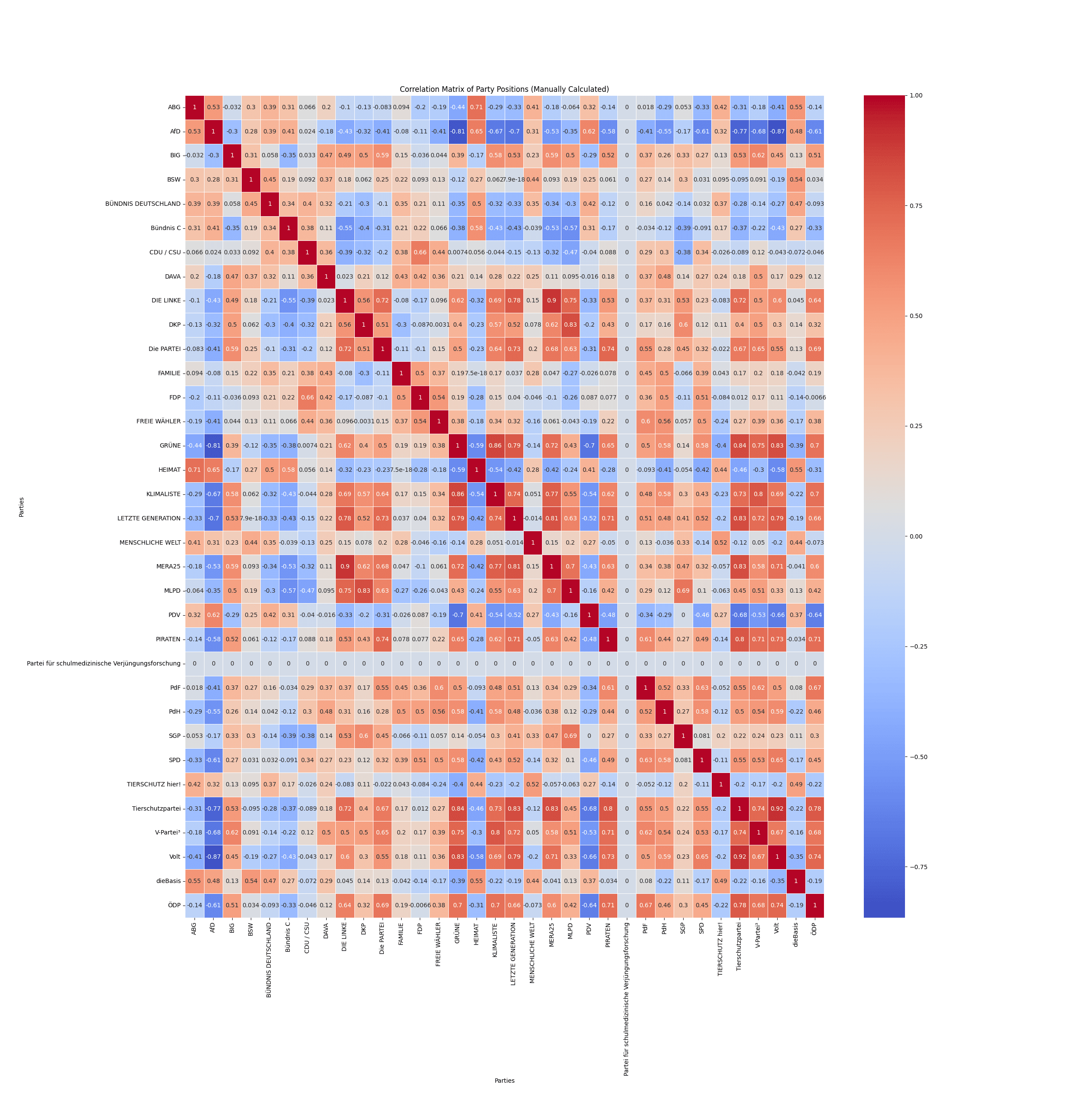
So thats a wrap for this post. Next step will be making a interactive representation of the correlation matrix.